분량도 분량인데 spyder에서 한영키가 안돼서 그거땜시 늦었음...
이게 한 글에 다 쓰기엔 좀 분량도 분량인데 이게 생각보다 설명이랑 코딩이랑 나뉘어있어서 이론편 실전편 나눕니다.

이건 clustering 중 하나인 hierarchical clusting. 오늘 할 게 대충 이런거다.
Cluster?
비슷한 특성을 가진 데이터 집단을 클러스터라고 한다. 데이터의 특성이 비슷하면 같은 클러스터, 다르면 다른 클러스터에 속한다. 클러스터링 하는 방법이 여러개가 있는데 여기서는 k-mean, k-median, k-medoid랑 hierarchical clustering에 대해 그냥 개 간단하게 설명하고 넘어간다.
Hierarchical clustering
앞에 k-들어가는 것과 달리 계층적 클러스터링이라고 한다. 계층 나누는 방식에 따라 Top-down과 Bottop-top으로 나뉜다.

젖산균을 젖산간균(Bacillus, 막대처럼 생긴 균)과 젖산구균(Coccus, 동그란거)으로 나눌 때
1) Top-down 방식은 젖산균이라는 큰 카테고리를 먼저 잡고 젖산간균과 젖산구균으로 나눈다.
2) Bottom-top 방식은 젖산간균과 젖산구균이라는 작은 카테고리를 잡고 그걸 젖산균으로 묶는다.
아, 참고로 말씀드리는거지만 유산균이나 젖산균이나 그게 그거임다. 젖산=유산이라..
K-들어가는 방법
이건 생각보다 정의 자체가 간단하다. mean은 평균(산술평균), median은 중앙값, medoid는 중앙자(계산하는 게 아니라 실제 데이터 값 중 대표값을 선정한다).
어떤 클러스터 내의 값이 81, 82, 83, 86일 때
산술평균: 83
중앙값: 82.5
으로 각각 계산을 통해 값을 도출하게 되지만 중앙자는 저 네 개의 데이터 중에서 값을 하나 골라서 거리를 계산하고 클러스터링하는 방식. 아, 산술평균이 우리가 일반적으로 생각하는 그 평균이다. (다 더해서 갯수로 나누는 그거)
Distance function
초장부터 날 당황하게 만든 그거 맞다.
Euclidean distance
Distance func. option: 'e'

유클리드 공간에서 두 점 사이의 거리를 나타내는 게 유클리드 거리. 따로 거리 함수를 지정해주지 않으면 이걸로 계산한다. 즉 Default값. 수학적인 정의는 뭔 소린지 모르겠지만 대충 피타고라스의 정리같은 거.
City-block distance(Manhattan distance)
Distance func. option: 'b'

식만 보면 이게 뭔 개소리지 싶겠지만 아래 그림을 보면 뭔지 대충 이해가 될 것이다.

초록색 선이 유클리드 거리이고, 나머지 선들이 맨하탄 거리(시티 블록 거리)이다. 저걸 좌표가 그려진 모눈종이라고 생각해보면, 유클리드 거리는 모눈이고 나바리고 대각선 ㄱㄱ하는거고 맨하탄 거리는 좌표 모눈 따라서 이동하는 것. 그래서 유클리드 거리가 좀 더 짧다.
대신 도시에서는 맨하탄 거리로 계산하는 게 낫다. 도시의 경우 저 하얀 부분이 대부분 건물인데 길 찾는다고 건물 뚫고 갈거임?
Pearson correlation coefficient
Distance func. option: 'c'
여기서부터 노션으로 정리하다가 사리나왔다. TEX 문법이 정말 (삐-)같거든...

피어슨 상관 계수는 두 변수간의 선형적인 상관관계를 계량한 것으로, 바 달린건 평균이고 시그마 달린건 표준편차다. 피어슨 상관 계수가 1이면 양의 상관관계, -1이면 음의 상관관계를 갖고 0이면 상관관계가 없다. 이를 이용해 구하는 피어슨 거리의 경우

이 공식으로 계산하므로 범위는 0~2. 2에 가까울수록 음의 상관관계, 0에 가까울수록 양의 상관관계를 갖고 1이면 상관관계가 없다.
Absolute value of the Pearson correlation coefficient
Distance func. option: 'a'
피어슨 상관 계수에 절대값 끼는거. 위 거리 공식에서 r에 절대값이 들어간다. 즉 0에 가까울수록 어쨌든 상관관계가 존재하는 것이다.
Uncentered correlation (cosine of the angle)
Distance func. option: 'u'
저거 사실 저렇게 검색하면 안나오니까 코사인 유사도(cosine similarity)로 검색하자.

코사인 유사도는 이렇게 구하고

저기 들어가는 시그마는 이런 식으로 구한다.

위키피디아에 나온 공식은 저거. 맨 아래 식을 이용해 거리를 구할 수 있고, 상관계수 자체는 -1에서 1까지의 값을 가지고, 거리는 피어슨때랑 마찬가지로 0에서 2까지의 값을 가진다. 어슨이형꺼랑 범위는 똑같은데 얘는 상관계수가 -1이면 반대인거고 1이면 완전 같은 경우. 0이면 독립정인 경우다.
Absolute uncentered Pearson correlation
Distance func. option: 'x'
위에 거리 공식에서 r에 절대값을 준 것.

그러니까 이거다.
Spearman’s rank correlation
Distance func. option: 's'
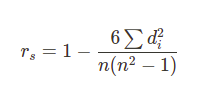

일단 이게 최종 계산 공식.

피어슨 상관 계수와 공분산을 쓰면 이렇게 계산한다. cov=공분산, rho=피어슨 상관 계수.
스피어맨 상관 계수는 피어슨 상관 계수와 달리 두 변수의 '순위' 사이의 통계적 의존성을 측정하는 척도이다. 두 변수 사이의 관계가 단조함수(주어진 순서를 보존하는 함수)를 통해 얼마나 잘 설명될 수 있는지를 평가한다. 즉 스피어맨 상관 계수는 변수에 순위가 있을 때의 피어슨 상관 계수. 단, 피어슨 상관 계수가 선형인 것과 달리 얘는 단조함수기 때문에 스피어맨 상관 계수가 1이라고 피어슨도 1인 건 아니다.
Kendall’s τ
Distance func. option: 'k'
켄달 타우라고 부른다. 대충

이게 타우인데... K랑 L이 뭐냐...
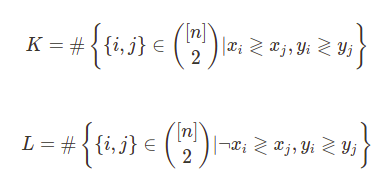

켄달타우도 스피어맨처럼 순위가 존재하는 변수에 대해 매길 수 있는데, K와 L은 각각 순위가 존재하는 두 변수 중 아무거나 픽했을 때 순위가 일치하는가 여부이다. 이게 무슨 소리냐... 체력장을 예시로 들어보자. 두 사람의 100미터 달리기와 1000미터 달리기의 기록을 비교했을 때 아래와 같은 가짓수가 나오게 된다.
1. 100m, 1000m 둘 다 빠르다
2. 100m, 1000m 둘 다 느리다
3. 100m에서는 빠르지만 1000m에서는 느리다
4. 100m에서는 느리지만 1000m에서는 빠르다
이 때 1, 2번같은 케이스를 concordant pair이라고 하게 되고, 변수 내에 concordant pair가 존재하면 K가 1, concordant pair가 아닌 케이스(3, 4번 케이스)가 존재하면 L이 1. L이 0인 경우가 많으면 타우(켄달타우)가 1에 가까워지고 K가 0인 경우가 많으면 타우가 -1에 가까워진다. 만약 0이라고요? 그러면 둘이 상관 없는거다.
L 공식에 저 꺾쇠? NOT이다.
'Coding > Python' 카테고리의 다른 글
| Biopython-Clustering 입력 인자 (0) | 2022.08.21 |
|---|---|
| Biopython으로 Clusting analysis 하기 (실전편) (0) | 2022.08.21 |
| Biopython으로 Sequence motif analysis 하기 (0) | 2022.08.21 |
| Biopython으로 Phylogenetic tree 그리기 (0) | 2022.08.21 |
| Biopython으로 PDB 탐방하기 (0) | 2022.08.21 |


